Abstract
I compare three sorts of case in which philosophers have argued that we cannot assert the Law of Excluded Middle for statements of identity. Adherents of Smooth Infinitesimal Analysis deny that Excluded Middle holds for statements saying that an infinitesimal is identical with zero. Derek Parfit contended that, in certain sci-fi scenarios, the Law does not hold for some statements of personal identity. He also claimed that it fails for the statement ‘England in 1065 was the same nation as England in 1067’. I argue that none of these cases poses a serious threat to Excluded Middle. My analysis of the last example casts doubt on the principle of the Determinacy of Distinctness. While David Wiggins’s ‘conceptualist realism’ provides a metaphysics which can dispense with that principle, it leaves no house-room for infinitesimals.
What connects Jesuit suppression of Jesuat mathematicians in seventeenth-century Italy, the issue of what happened to England in 1066, and a recently departed Oxford philosopher’s speculations about brain bisection? This may sound like an excessively contrived question from Round Britain Quiz, but it has, I shall argue, a perfectly sensible answer: the connection is the logic of identity. What is more, new light may be cast on the last two topics on the list by thinking about them in the context suggested by the rather less familiar first.
1. Infinitesimals
The founders of the calculus in the seventeenth century made essential use of infinitesimal quantities – that is, of quantities whose absolute values, while not necessarily being identical with zero, are smaller than any finite value. Thus Isaac Barrow wrote of ‘linelets’ and ‘timelets’; these are crucial to his method for calculating the slope of tangents in Lectiones Geometricae (1670). His student, Newton, wrote of ‘evanescent quantities’; these, too, are essential to his development of the calculus. The same holds good of Newton’s great rival, Leibniz, who wrote of ‘quantités inassignables’.
In all of this, Barrow, Newton, and Leibniz were following a lead that Italian mathematicians had provided earlier in the seventeenth century. Galileo’s argument for his law of falling bodies (the distance travelled in time t by a body uniformly accelerating from rest at rate a equals ½at 2) treats the area under a velocity-time curve as composed of infinitely many infinitesimally thin lines. His student Cavalieri extended this ‘method of indivisibles’ to determine the area inside a spiral, and Cavalieri’s pupil Torricelli deployed and extended the method in his Opera Geometrica (1644), a work studied closely by Wallis, Newton, and Leibniz. Unfortunately for the Jesuat mathematicians inspired by Cavalieri’s Geometria Indivisibilibus, the Jesuits anathematized infinitesimals as heretical, and their view eventually prevailed in Italy. In his book Infinitesimal, Amir Alexander argues convincingly that this edict was partly responsible for moving the centre of activity in mathematics and physics away from the sunny squares of Padua and Bologna to the damper environment of the English fens.1
In disparaging infinitesimals, the Jesuits have had more recent allies. Berkeley derided them as ‘ghosts of departed quantities’.2 Russell − not usually a friend of the Society of Jesus − dismissed them as ‘unnecessary, erroneous, and self-contradictory’.3 The charge of self-contradiction was refuted by Abraham Robinson when he created non-standard analysis but his conception of infinitesimals, resting as it does on twentieth-century model theory, lies at some distance from anything that the founders of the calculus could have had in mind.4
A more recent development − Kock and Lawvere’s Smooth Infinitesimal Analysis (SIA) − takes us closer to the geometric intuitions that underpinned the founders’ work. In his Analyse des Infinements Petits (1696), De L’Hôpital postulated that ‘a curved line may be regarded as made up of infinitely small straight line segments’, thereby making explicit Barrow’s notion of a ‘linelet’. De L’Hôpital’s postulate provides, indeed, a key axiom of SIA:
The Principle of Microstraightness: For any smooth curve C and any point P on C, there is a non-degenerate segment of C (i.e. a segment of C which does not reduce to a single point) which is straight around P; that is, C is ‘microstraight’ around P.5
If we apply this Principle to the parabola y = x 2 at the origin, we may infer that there is a non-degenerate set Δ of magnitudes ε such that ε2 = 0. That is, there is a non-degenerate set of nilsquare infinitesimals.
The Principle of Microstraightness is the heart of SIA. It tells us that a smooth curve is made up, not of points, but of infinitesimal straight lines. This is apt to shock those who have become accustomed to the modern, punctiform conception of a curve. After a talk in which I had expounded the axioms of SIA, a prominent American logician asked me why he should take seriously the suggestion that a sufficiently small sector of a pizza is, in fact, a triangle. Perhaps the best answer is that SIA combines with elementary geometry to yield simple but rigorous proofs of results that would otherwise need more advanced methods. Consider the figure overleaf, in which ε is an infinitesimal:
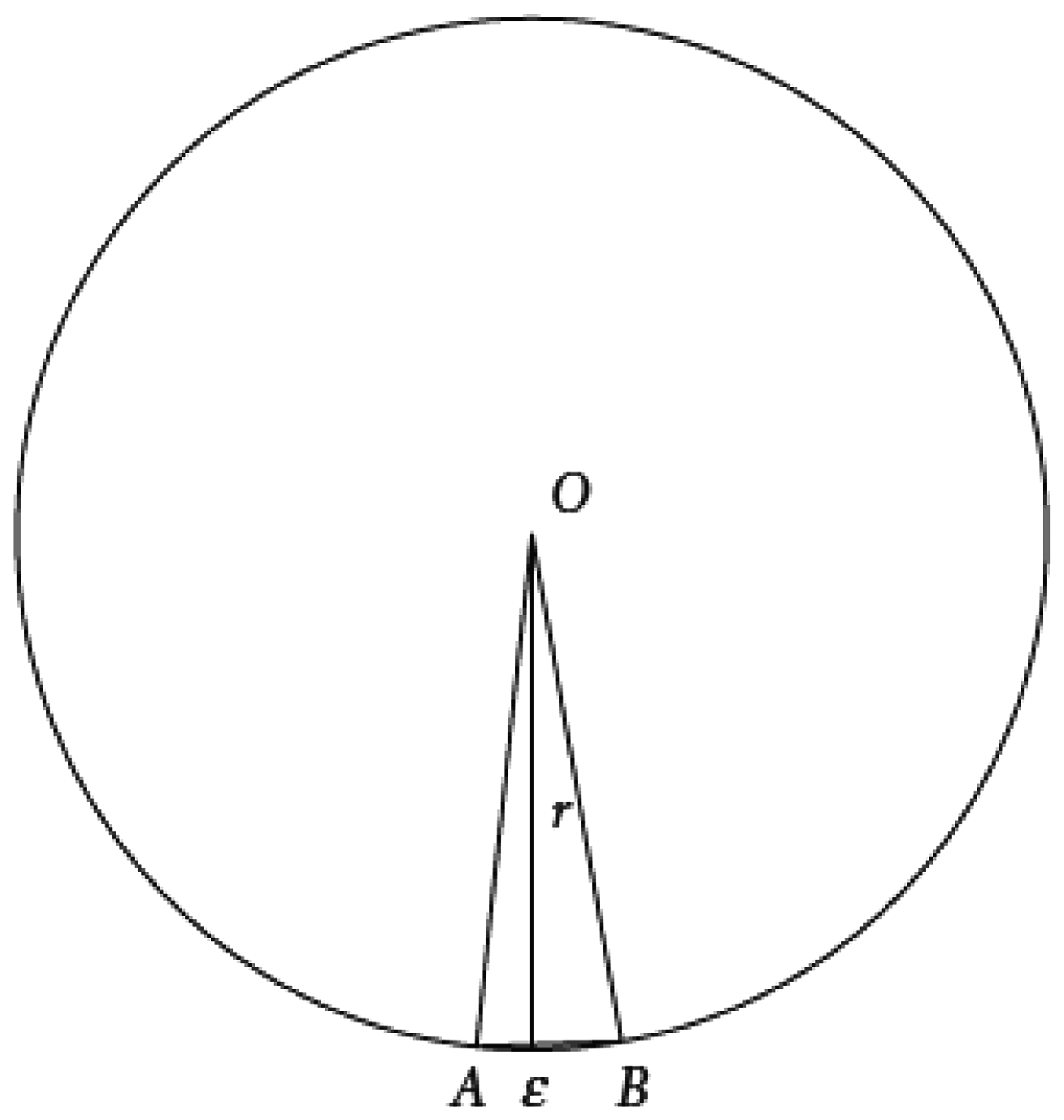
Because the segment AB is microstraight, the region OAB is a triangle of height r, and base ε. Hence its area is ½rε. Since its circumference is 2πr, the whole circle will be made up of 2πr/ε of these triangles. In this way, we can prove very simply that the total area of the circle is ½rε × 2πr/ε = πr 2. For the benefit of my logician colleague, one might add that this result yields in turn the volume of a cylinder of radius z and height a: pi.z.z.a.
Nilsquares are elements of the ‘smooth’ real number-line, R. We are not to think of R as a set of points. Rather, we are to conceive of it as Euclid conceived of the continuum − namely, as a nest of lines, items with length but no breadth. SIA then postulates that there are operations of addition, +, and multiplication, . , on R, and a relation <, with respect to which R constitutes an ordered field. In particular, SIA postulates that any quantity in R that is not identical to zero has an inverse under the . operation, i.e. a reciprocal.
We can then show that any nilsquare infinitesimal is smaller than any ‘regular’ (i.e. finite) real number:
2. The Law of Excluded Middle
There is, alas, a price to be paid for this elegant and simple theory. The Law of Excluded Middle (LEM) is a principle of classical logic. It entitles us to assert ‘Either A or not A’, in symbols ⌈A ∨ ¬A ⌉, for any statement A. Where ε is an arbitrary nilsquare infinitesimal, take A to be the identity statement ‘ε = 0’. If Excluded Middle always held, we could assert ⌈ε = 0 ∨ ¬(ε = 0)⌉. In SIA, however, the second alternative yields a contradiction. From the hypothesis that ¬(ε = 0), we may infer that ε has a reciprocal, i.e. there exists a y such that ε.y = 1. But then 0 = 0.y = ε2.y = ε.(ε.y) = ε.1 = ε. Given LEM, then, SIA entails that each nilsquare is identical with 0, and the Principle of Microstraightness is refuted: there is no non-degenerate collection of nilsquares.
For this reason, proponents of SIA formalize it as a theory in intuitionistic logic, a system where not all instances of LEM are assertible. Indeed, the argument of the previous paragraph shows that the theory needs to be formalized in a logic in which we are not entitled to assert Excluded Middle for certain statements of identity, e.g. ‘ε = 0’.
In fact, SIA demands more radical departures from classical logic. We have just seen that it generates what are called weak counterexamples to LEM; that is, there are instances of LEM which, if asserted, would contradict the theory. But there are also theorems of SIA which flat out contradict classical logical truths. A theorem of the classical predicate calculus is Excluded Middle for Properties (EMP):
An instance of EMP is ⌈∀ε∈Δ (ε=0 ∨ ¬(ε=0)⌉. As we have seen, ⌈¬(ε = 0)⌉ yields a contradiction in SIA, so SIA entails ⌈∀ε∈Δ (ε=0)⌉ in both intuitionistic and classical logic. However, the axioms of SIA also entail that the nilsquares are non-degenerate:
⌈¬∀ε∈Δ (ε=0)⌉.6 Since the hypothesis ⌈∀x (x = 0 ∨ ¬x = 0)⌉ entails a contradiction, we may conclude even in intuitionistic logic that ⌈¬∀x (x = 0 ∨ ¬x = 0)⌉ is a theorem of SIA. Thus SIA proves the negation of an instance of EMP.
That an intuitionistic theory should prove such a result is not unprecedented; the same is true of intuitionistic analysis, i.e. the intuitionist’s theory of real numbers. However, the explanation for this radical departure from classical logic is quite different in the two cases. In the case of analysis, the explanation lies in the intuitionist’s rejection of completed infinities. The classical mathematician identifies a real number such as π with its complete decimal expansion. For the intuitionist, there is no such thing as a complete infinite expansion; in the case of π we simply have a rule for further expanding the sequence 3.14159…. Brouwer realized that he would be left with only a ‘poor and anaemic’ ersatz for the classical continuum if he recognized only those real numbers whose decimal expansions are given by a rule, and in his ‘Second Act of Intuitionism’ he postulated ‘freely proceeding infinite sequences of mathematical entities previously acquired’ (such as natural or rational numbers).7 It is these ‘free choice’ sequences which ensure a rich intuitionistic continuum, and it is the axioms describing their behaviour which yield theorems that contradict classical validities. The axioms in question come in various strengths, but even the weakest of them, the so-called Local Continuity Principle, yields ⌈¬∀x (x = 0 ∨ ¬x = 0)⌉.8
Matters are different with SIA. As we have seen, it also yields ⌈¬∀x (x = 0 ∨ ¬x = 0)⌉, but not because it rejects the completed infinite. Instead, the result arises because the infinitesimals it postulates do not stand to zero in a determinate relation of identity or distinctness: we cannot say that a nilsquare infinitesimal is either less than zero, identical with zero, or greater than zero. Similarly, given infinitesimals ε and δ, we cannot say that either ε is less than δ, or ε is identical with δ, or ε is greater than δ. Any attempt to place a nilsquare in a determinate order relation to zero, or to another nilsquare, leads to contradiction.
This raises an interesting philosophical question. Elegant as SIA may be, we would not normally accept a theory which contradicts our standard logic, but perhaps classical logic is wrong to count EMP as a law. Perhaps it is too restrictive in eliminating from consideration theories that postulate indeterminacy in respect of identity or distinctness. In considering these possibilities, it is natural to ask whether there are other plausible examples of such indeterminacy. Is EMP a dead hand which stops us from giving a correct description of some other cases − particularly cases which lie at some distance from the enticing but perhaps incoherent domain of nilsquare infinitesimals?
3. Parfit’s fission case and Excluded Middle
At this juncture, it helps to bring Derek Parfit into the discussion. Here is a passage from his famous paper, ‘Personal Identity’:
My targets are two beliefs: one about the nature of personal identity, the other about its importance.
The first is that in these cases [i.e. certain problem cases, soon to be described] the question about identity must have an answer.
No one thinks this about, say, nations or machines. Our criteria for the identity of these do not cover certain cases. No one thinks that in these cases the questions ‘Is it the same nation?’ or ‘Is it the same machine?’ must have answers.
Some people believe that in this respect they are different. They agree that our criteria of personal identity do not cover certain cases, but they believe that the nature of their own identity through time is, somehow, such as to guarantee that in these cases questions about their identity must have answers. This belief might be expressed as follows: ‘Whatever happens between now and any future time, either I shall still exist, or I shall not. Any future experience will either be my experience, or it will not.’…
I cannot see how to disprove this first belief. I shall describe a problem case. But this can only make it seem implausible.9
The beliefs that Parfit is challenging in this passage appear to be instances of Excluded Middle: ‘Either I shall exist at time t or I shall not exist then’; ‘any future experience will either be my experience or it will not be’. So Parfit seems to be deeming one of the laws of classical logic to be implausible. The instances of LEM which he takes to be problematical involve existence (‘I shall exist at time t’) and ownership of experience (‘Any future experience will be mine’) rather than identity. As we shall see, though, his leading problem case is one in which it is, prima facie, indeterminate whether a certain statement of identity is true or false. So his case provides an example of what we are seeking.
The case in question is a development of David Wiggins’s ‘fission scenario’.10 My brain is divided and each half is put in a different brainless body. Both the resulting people − call them A and B − have my character and apparent memories of my life, and pursue my goals. To ensure complete symmetry, let us also stipulate that the brainless bodies are those of identical twins, so there is no respect in which one of A or B resembles me more than the other does. The question Parfit then poses is: do I survive this procedure? There are, he thinks, only three possible answers:
(1)I do not survive;
(2)I survive as one of the two people;
(3)I survive as both.
Parfit rejects options (1) and (2). It is clear, he claims, that I would survive if one half of my brain were disposed of and the other half were put into a brainless body in such a way that the resulting creature had apparent memories of my life and continued to execute my intentions and plans. He then rejects (1) on the grounds that a double success is not a failure. He rejects option (2) because in the specified scenario the situations of A and B are completely symmetrical. It would then be entirely arbitrary to maintain that I survive as A (say) but not as B.
Whatever we think about these claims, it is Parfit’s analysis of the third option that is relevant to the logic of identity. Option (3), he maintains, is the correct description of the fission scenario: I survive as both A and B. The question is what this description could mean.
If survival implies identity, Parfit argues, we cannot say that I survive as A and also that I survive as B. For if survival implies identity, that would entail that I am identical with A, and also that I am identical with B. Identity is a symmetric and transitive relation, so these claims would in turn entail that A is identical with B. And that is clearly not the case: A and B are distinct persons.11
On the assumption that survival implies identity, then, the only coherent version of option (3) is one where I survive as a composite or fusion of A and B − that is, as a person with two bodies and a divided mind. Somewhat as the Pope’s crown is made up of three pieces of metal which had, and could have again, independent existence as crowns, so I am identical with the composite of person A and person B. Parfit allows that we can make sense of one person’s having a divided mind, at least in cases where the division is only for a short period.12 But when applied to the fission scenario, he acknowledges, the thesis that I am identical with the composite of A and B ‘keeps the language of identity only by changing the concept of a person’, and in an objectionable way (op. cit., 8). A duel to the death between A and B involves an unholy trinity of persons, but our ordinary notion of person offers no guidance as to how many survive (op. cit., 8 n.8).
Parfit draws two morals from his discussion of the fission scenario:
Thesis 1: We should admit that some questions about identity have no answers.
Thesis 2: We should separate questions about survival from questions of identity. In particular, we should recognize that ‘I survive as A’ does not entail ‘I am identical with A’.
Thesis 2 opens up the logical space needed to maintain that questions about personal survival have answers even in circumstances where the corresponding questions about identity do not.
Parfit’s argument for Thesis 2 is clear, at least in outline. Option (3), he contends, is the correct description of the fission scenario: I survive as both A and B. But that correct description is reduced to incoherence, or to an objectionable revision of the concept of a person, if survival implies identity. Accordingly, the key philosophical task is to articulate a sense in which someone may survive as two persons. This means finding a sense for ‘Will I survive?’ other than ‘Will there be some person alive who is identical with me?’
The breach that Parfit tried to open between survival and identity is, I think, what readers of his paper have found most exciting. Having made the breach, one can allow (for example) that survival is a matter of degree, even while acknowledging that identity is all-or-nothing. For present purposes, though, what matters is Thesis 1, not Thesis 2. We are not concerned with the correct account of personal survival. Rather, we are addressing the question of whether Parfit’s discussion casts any doubt on the Law of Excluded Middle as it applies to statements of identity. I wish to argue that it casts no doubt on this at all. For, in fact, Thesis 2 undermines the argument for Thesis 1.
My reason for saying this is simple. Suppose we succeed in articulating the sense in which I survive as both A and B. Since survival does not imply identity, it is then open to us to maintain that I am not identical with A, and also not identical with B. What is more, Parfit’s discussion provides a compelling argument for precisely this conclusion. For suppose I were identical with A. As Parfit notes, if that were so there would be equally good reason to hold that I am identical with B, in which case A would be identical with B. But A is not identical with B, so I am not identical with A. Thus the question of identity, ‘Am I identical with A?’ does have an answer, viz. ‘No’. The question ‘Am I identical with B?’ has the same negative answer, for a precisely parallel reason. When the issue is thought through, then, Parfit’s analysis of the fission scenario provides absolutely no support for Thesis 1. Once we have separated questions of survival from questions of identity − in particular, once we have seen that ‘I survive as A’ does not entail ‘I am identical with A’ − it is entirely consistent to maintain that I survive as both A and B while being identical with neither. Moreover, there is a powerful argument for holding precisely this position.
Just for this reason, Parfit’s analysis poses no threat to the Law of Excluded Middle, as this applies to statements of identity. The disjunction ‘Either I am identical with A, or I am not’ is straightforwardly true because its second disjunct is true. The same goes for the disjunction ‘Either I am identical with B, or I am not’. For all Parfit’s discussion of the fission scenario shows, then, Excluded Middle is what Frege thought any logical law ought to be: a ‘boundary stone fixed in an eternal foundation, which our thinking can overflow, but never displace’.13
4. The identity of nations
Radical as they are in many respects, then, Parfit’s speculations about personal identity offer no real challenge to LEM and hence no support that an adherent of nilsquare infinitesimals can pray in aid. But what about the more homely examples he mentions in the passage quoted? ‘No one’, he writes, ‘thinks that…the questions “Is it the same nation?” or “Is it the same machine?” must have answers.’ Later in the paper, he gives an example of a question of the former kind ‘in which, for quite unpuzzling reasons, there is no answer to a question about identity. (Consider “Was England the same nation after 1066?”)’.14
We ought to grant to Parfit two points. First, even though it is a fact that England in 1063 was the same nation as England in 1065, this is not a brute fact. The fact in question is determined, or constituted, by a host of lower-level facts: that the structures of government persisted between 1063 and 1065; that there was no abrupt change in the personnel exercising political authority between those dates; and so forth. The second point to be granted is this. Circumstances may arise in which the totality of relevant lower-level facts fails to determine either a positive or a negative answer to a question of national identity. Parfit’s question is a plausible example of such a case. Much of the Anglo-Saxon nobility was killed at the Battle of Hastings, so 1066 saw an abrupt change in the personnel holding high political office in England. On the other hand, the Conqueror initially tried to govern within the structures familiar to his new subjects, maintaining (for example) the shire courts and the sheriffs, and using his curia as the successor to the Saxon witan. Even if we were given all the facts concerning the structure of England’s government and who was exercising political and legal authority in the period between 1065 and 1067, they would not determine an answer to the question ‘Was England the same nation after 1066?’
What this analysis suggests is that there is no determinate answer to that question, so that we are not entitled to assert the following disjunction:
(4)Either it is determinately the case that England in 1065 was the same nation as England in 1067, or it is determinately the case that England in 1065 was a distinct nation from England in 1067.
This suggests a way in which the present case could be turned to cast doubt on certain instances of Excluded Middle for identity statements. For let us suppose that both identity and distinctness must be determinate, if they obtain at all. More precisely, let us suppose that, for any objects x and y, we may assert
(DI) If x = y, then it is determinately the case that x = y
and
(DD) If ¬(x = y), then it is determinately the case that ¬(x = y).
Now suppose that we were entitled to assert the following instance of Excluded Middle:
(5) Either England in 1065 was the same nation as England in 1067, or England in 1065 was a distinct nation from England in 1067.
By instantiating the variables ‘x’ and ‘y’ in DI and DD with the terms ‘England in 1065’ and ‘England in 1067’, we could then deduce (4) from (5). Ex hypothesi, though, we are not entitled to assert (4). Accordingly, we are also not entitled to assert (5).
Is there good reason to accept both the Determinacy of Identity and the Determinacy of Distinctness? Following the model of Ruth Barcan Marcus’s celebrated proof of the necessity of identity, Gareth Evans gave a simple and powerful argument for DI.Footnote15 Suppose that x is identical with y. Then anything true of y is also true of x. Now one thing that is true of y is that it is determinately identical with y. So it must also be true of x that it is determinately identical with y. That implies that it is determinately the case that x is identical with y.
Simple and powerful though this argument may be, it is open to challenge. Some have resisted its final step by distinguishing the claim, concerning the object x, that it is determinately identical with y, from the argument’s eventual conclusion that x = y holds good determinately.16 For the sake of argument, though, let us grant DI. We still have to ask what might justify DD.
The most influential argument for the Determinacy of Distinctness is due to Timothy Williamson.17 It may be presented in formal dress as follows, in which ‘□’ symbolizes ‘it is determinately the case that’:
1.x = y → □(x = y) DI
2.¬□(x = y) → ¬(x = y) Contraposing (1)
3.□(¬□(x = y) → ¬(x = y)) What is proved by logic is determinate
4.□¬□(x = y) → □¬(x = y) Applying modal rule (K) to (3)
5.¬(x = y) → □¬□(x = y) Brouwerian Law for □
6.¬(x = y) → □¬(x = y) (4), (5) hypothetical syllogism
The rule (K) that is applied in reaching line (4) licenses the inference from □(A → B) to □A → □B, for arbitrary A and B. The Brouwerian Law used at line (5) asserts that ¬A → □¬□A, for arbitrary A. Given these principles, (6) follows from (1), which is to say DD follows from DI.
Should we accept the operative modal principles, though? When ‘□’ means ‘it is determinately the case that’, rule (K) is compelling: from the premisses ‘It is determinately the case that if A then B’, and ‘It is determinately the case that A’, we may infer ‘It is determinately the case that B’. But what of the Brouwerian Law? If it is not the case that A, is it always determinately the case that it is not determinately the case that A?
The answer is far from obvious. What is clear, though, is that appealing to the Brouwerian Law in the present dialectical context is entirely question-begging. On any view, the converse of DI is true: if it is determinately the case that x = y, then x = y. Given DI, then, which is after all a premiss of Williamson’s argument, ‘x = y’ is equivalent to ‘□(x = y)’. Moreover, if DI and its converse are true at all, they are surely determinately true. Hence, by (K), the equivalence between ‘x = y’ and ‘□(x = y)’ itself holds determinately and we may substitute ‘x = y’ for ‘□(x = y)’ within the scope of ‘□’. That is to say, line (5) of the derivation, viz. ‘¬(x = y) → □¬□(x = y)’, is equivalent to line (6), viz. ‘¬(x = y) → □¬(x = y)’. In other words, the instance of the Brouwerian Law cited at line (5) simply assumes what is to be proved.
Is there anything to be said for a position which accepts DI but does not accept DD? David Wiggins took such a position in an essay of 1986.18 Wiggins was later persuaded by Williamson’s argument to accept both DI and DD.19 As I have just explained, though, that argument offers no independent support for DD. Is there anything to be said for Wiggins’s original view?
I think there is. As in many of his other writings about objects and identity, Wiggins proposes a ‘conceptualist’ or ‘conceptualist realist’ metaphysics whereby ‘x is a genuine object if and only if, in a sense of “single out” to be gradually refined, x can in principle be singled as this such-and-such or this so-and-so’.20 Accepting DI without accepting DD coheres nicely with that metaphysics, because nothing then ‘prevents thinkers from delimiting definitely what they single out, and counting as quite clear what they have singled out, without making absolutely everything definite about the frontier between that thing and that which is not that thing. For if we accept [DI] without [DD], then it can be definite what a thing is without its needing to be definite in every way and at every point what it is not. And why not accept [DI] without [DD]? After all, whatever thing you take, there is one thing it is, even if there are limitlessly many things that it is not’.21
What, on this view, is the answer to Parfit’s question about England? We should say the following. In a case where the lower-level facts − the facts about the structure of the government and the continuity of its office-holder − do not determine that the England of 1065 was the same nation as the England of 1067, then we should judge that the England of 1065 was not determinately the same nation as the England of 1067. Given DI, we should be prepared to contrapose and to conclude from this that the England of 1065 was not the same nation as the England of 1067. ‘If the case is not good enough, then what [DI] reminds us is simply that the [nations] are not the same. Why object to that?’22 One potential objection has been answered. It would indeed be objectionable if one could infer from the thesis that the nations are not the same that they are determinately not the same, for that would be to say that the question has a determinately correct answer after all. Without DD, though, we are not entitled to make that inference. Accordingly, by refraining from accepting DD we can make logical room for the difference between identity questions which have determinate answers and those which do not.
5. Infinitesimals revisited
Where, finally, does this analysis leave the Law of Excluded Middle for statements of identity, and the case for nilsquare infinitesimals?
It should be clear that the recommended position poses no threat at all to the Law. Where ‘a’ abbreviates ‘England in 1065’ and ‘b’ abbreviates ‘England in 1067’, we shall not be entitled to assert
(6)Either □(a = b) or □¬(a = b).
In this way, we gratify the intuition that Parfit’s question has no definite answer. However, there is nothing to stop us from asserting the relevant instance of Excluded Middle, which is
(7)Either (a = b) or ¬(a = b).
To infer from (7) to (6) we would need both DI and DD. On the recommended position, we do not have the latter principle, so we can consistently assert (7) while refraining from asserting (6).
As for nilsquares, the deviation from classical logic which SIA requires gains no support from our analysis of this other case where a question of identity lacks a determinate answer. In fact, on the conceptualist metaphysics of objects that is being recommended, matters are even worse for SIA. That theory treats nilsquares as objects, things over which first-order variables range. Given conceptualism, this implies that a thinker must, in principle, be able to single out a nilsquare. It is, however, doubtful whether this is possible even in principle. Singling out a number involves placing it in order relations to other numbers: thus singling out the real number π involves, among other things, coming to know that it lies in the interval between 3.1415 and 3.1416. As we saw, however, SIA precludes (on pain of collapsing into contradiction) giving answers to questions that naturally arise about the order relations between nilsquares and other numbers. For the reasons explained in §2, where ε and δ are nilsquares we shall get contradictions if we return either affirmative or negative answers to ‘Is ε greater than zero?’ or ‘Is ε greater than δ?’ Smooth Infinitesimal Analysis has some superficially attractive features. However, the nilsquares that it postulates resist being singled out. From the perspective of a conceptualist realist metaphysics, then, it is doubtful whether the theory in the end makes sense.
Footnotes
This paper is a record of a talk I gave at a number of schools in the years 2014-18 with the aim of showing how a joint honours degree in mathematics and philosophy could offer students more than the sum of its parts. Friends have suggested that a wider readership might enjoy it. Each of the topics treated is the subject of a vast literature. I have not, though, come across another paper which explores the relations between them.
References
-
Author
Ian Rumfitt is Professor of Philosophy and Senior Research Fellow at All Souls College, University of Oxford.
-
First published
Philosophy, Volume 94, Issue 4, October 2019, pp. 513 - 528
DOI: https://doi.org/10.1017/S003181911900010X
